李博楠

中交路橋科（kē）技有限公司

摘 要（yào）：以位於季凍（dòng）區內的河北（běi）省張承高速路基填土（tǔ）為研究（jiū）對象，在設計滿足實（shí）際工況下的凍融循環的（de）試驗基礎上，采用室內動（dòng）三軸（zhóu）試驗，分析不同影響因（yīn）素包括凍（dòng）融循環次數、壓實度、圍壓及振動頻率下各項動力（lì）學參數的變化情況，應用多元非線（xiàn）性回歸的線性化（huà）分析方法，建立動黏聚（jù）力（lì）與最大動彈性（xìng）模（mó）量的回歸公（gōng）式，識別路基（jī）填土在凍融循環作用後的動載作用下的動力學特性變化規律，為解決季凍區高速公路路基填土凍融病害提供相關數據和理論支持。

關鍵詞：凍（dòng）融循環;高速公路;路基填土;動力學;動三軸試驗;

作者簡介：李博楠(1994-),男，碩士，主要研究（jiū）方（fāng）向：道路工程材料。;

引言

張家口—承德高速公路地處河北省北部，屬季凍區域，隨著冬奧會的來臨，作（zuò）為首都（dōu）環線的重要組成部分，其通行量日益提高，而氣溫的變化尤其是凍融作用引起（qǐ）的路基路麵（miàn）病害也（yě）越來越嚴重，路（lù）基因凍脹、融沉而導致的直接或間接病害影（yǐng）響（xiǎng）了高速公路的服務水平和（hé）通行質量，加大了養護維修成本，有必要對張承高速公路的（de）路（lù）基填土（tǔ）在（zài）凍融循環作用（yòng）及行車動荷載作用下發生的（de）強度、變形等物理力學特性展開相關（guān）研究。

高速（sù）公路路基在經受凍融循環（huán）作（zuò）用時，不僅承受著內部的溫度應力和上部的自重靜載，還要承受來（lái）自過往車輛行駛所帶來（lái）的動（dòng）荷載。研究（jiū）路（lù）基填土在（zài）凍融循環作用（yòng）及動載（zǎi）作用下的動力學特性，對進一步了解土體在凍融循環作用下的實際力學行為具有非常重要的意（yì）義。

1 試驗用（yòng）土（tǔ）的（de）基本性質

選取位於張承高速（sù）沿線具有一（yī）定代表性的（de）土樣，采用液塑限聯合測定儀進（jìn）行液塑限的測定，根據塑性圖法對本次試驗（yàn）土樣進行工程分類的判定，確定本次所選擇土樣的（de）液限為31.2%,塑性指數Ip為13.2,落在A、B交（jiāo）點的左上方即CL區，因此可以判（pàn）定本次試驗用土樣為（wéi）低液限黏性土。

2 擊實試驗

選擇落錘式電動擊實儀的方法進行試驗，采用重型（xíng）擊實，分（fèn）五層每層27擊。取（qǔ）均勻性良好的試驗（yàn）用土樣5組，按照相鄰含水率之差（chà）2%～4%的要求分別配置成不同含水率的土樣試件進行（háng）試驗。確定最佳含水率為11.2%,最大幹密度為1.95。

3 試驗方法

3.1 凍融循環試（shì）驗

結（jié）合張承高速路線沿線氣候變化規律，擬定環境負溫-10℃,融化時（shí）溫（wēn）度統一設定（dìng）為20℃。考（kǎo）慮實際工況（kuàng），土體的凍（dòng）結過程主要為單向凍結，為更接近工程實際，將製備好的最佳（jiā）含水率下的土樣試件用塑料薄膜包（bāo）裹後放置在帶有孔位的泡沫塑（sù）料板（bǎn）中模擬土在路基中受凍時的物理狀態，將土樣與泡沫板一同放入冷凍箱及恒溫（wēn）箱（xiāng）中（zhōng）進行試驗操作（zuò）。結合當地的實際晝夜溫（wēn）度（dù）變化及凍融情況，選擇凍結—融化時間周期為24h, 其中凍、融分別取12h。對凍融次數選擇分別為1次（cì）、3次、5次、7次和11次。

為討論不同層次或不同密（mì）實程度下土（tǔ）基受凍融作用影響的變化情（qíng）況，選擇壓實（shí）度92%、95%、98%分（fèn）別進行正交試（shì）驗。

3.2 動力學試驗

采用TAJ-20型電液伺服動（dòng）(靜)三軸試驗儀。本次試驗采用三種（zhǒng）振動頻率（lǜ）f=0.5Hz、f=1Hz、f=5Hz的正弦波的形式輸入，同時為簡化操作，選擇動力加（jiā）載方式為單（dān）向加載，當動應變累計（jì）達到5%時停止。

各組試驗的具體參數（shù）如表1所示。

表（biǎo）1 試件各項（xiàng）條件指標

各組（zǔ）試件均在30、60和90kPa圍壓（yā）水平下進行試驗。圍壓的加載增（zēng）速設定（dìng）為1kPa/s, 待圍壓增至（zhì）目標（biāo）值後，調整正向應力使（shǐ）其與圍壓相（xiàng）同，待試件在等壓條件下固結24h後（hòu）關閉排水（shuǐ）閥；在（zài）不排水條件下（xià）沿（yán）試件軸向施加σd偏應力，然後施加同樣值（zhí）的動應力半正弦波進行（háng）動力加載。

4 動力學參數的變化規律研究

4.1 動強度指（zhǐ）標（biāo）

以破壞（huài）振動次數Np=100次、1000次和10000次為研究條件，通過動強度曲線確定各破壞時（shí）振動次數Np和對應的（de）動應力幅值（zhí）σd,繪製摩爾應力包線，確定土樣的動摩擦角和動黏聚力cd。

4.1.1 凍（dòng）融循環次數的影響

同一壓實度(K=95%)、同一振（zhèn）動頻率(1Hz)不（bú）同凍融循環次數下動強度指標cd 、φd值如圖1至圖2所（suǒ）示。

圖1 動內摩擦角與凍融循環次數關係曲線

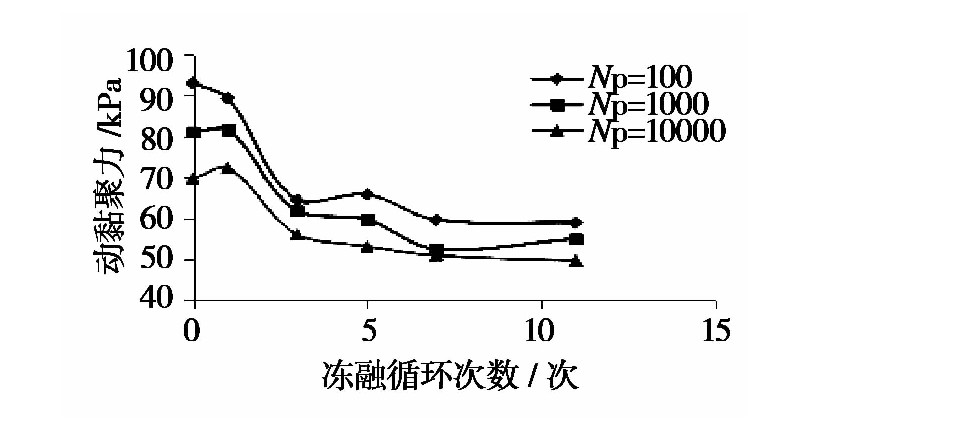
圖2 動黏聚力與凍融（róng）循（xún）環次數關係曲線（xiàn）

試件在經受（shòu）第（dì）1次（cì）凍融循環作（zuò）用後，其動內摩擦角均有一（yī）定程度的下降（jiàng），而（ér）後隨（suí）著凍融循環次數的增加，內（nèi）摩擦角在27°～32°間波動。當處於同一凍融循環次數時，隨著（zhe）破壞振動次數的增加，動內摩擦角有（yǒu）一定程度降低；而隨著凍融循環（huán）作用次數的（de）增加，動（dòng）黏聚力值逐漸衰減並趨（qū）於穩定，由於土樣（yàng）試件內部在經受第1次凍融循（xún）環作用，內部孔隙結構發生了趨（qū）於（yú）特征化的重新分布（bù），在外部振動（dòng）加載作用（yòng）的影響下，孔隙結構（gòu）被填充或壓密（mì），而在凍融循環作用次數繼續增加後，孔隙結構再次被凍脹—水分排出作用改變或影（yǐng）響，內部土粒間作用力持續（xù）降（jiàng）低。

4.1.2 壓實（shí）度的影響

不同（tóng）壓實度下土樣的動強度指標分別如圖3至（zhì）圖4所示（shì）。

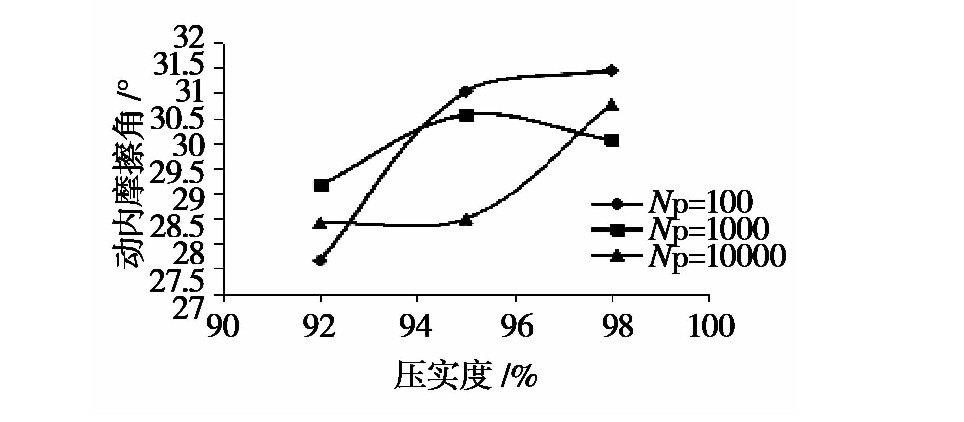
圖3 不同壓實度下動（dòng）內摩擦（cā）角值

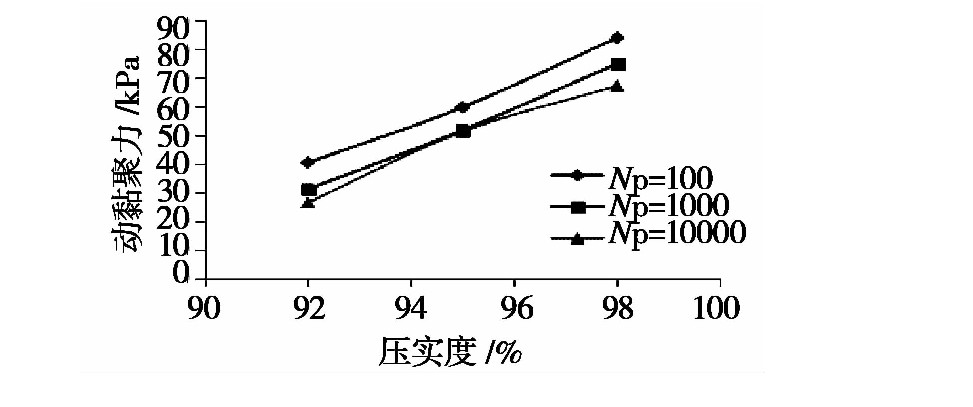
圖4 不同壓實度下動黏聚力值

不同壓實度下內摩擦角曲（qǔ）線變化規律性較差；而動黏聚力隨壓實度變（biàn）化的規律性較強（qiáng），隨（suí）著壓實度的提（tí）高，動黏聚力類似線性（xìng）增長。當試件的壓實度一定時，隨著破壞振動次（cì）數的增加，其動黏（nián）聚力有所降低。

4.1.3 振動頻率的影響

不同振動頻率下土樣的動強度指標分（fèn）別如（rú）圖5至圖（tú）6所示。

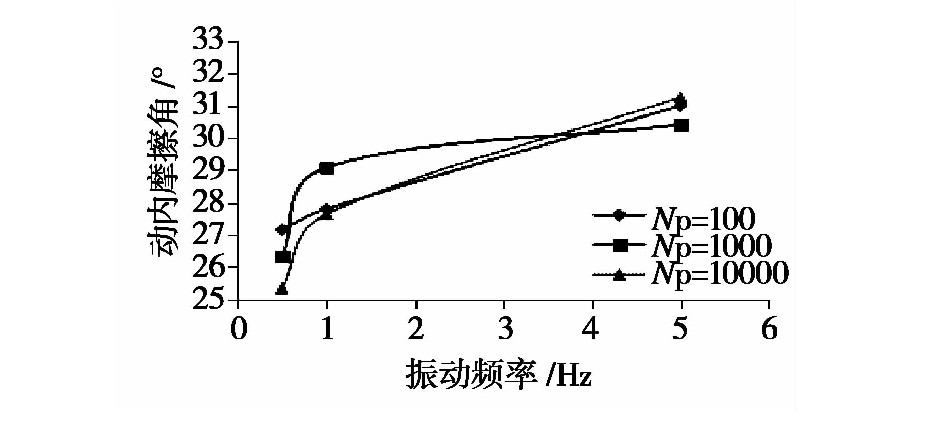
圖5 不同振動頻率下動內摩擦角值 下載原圖

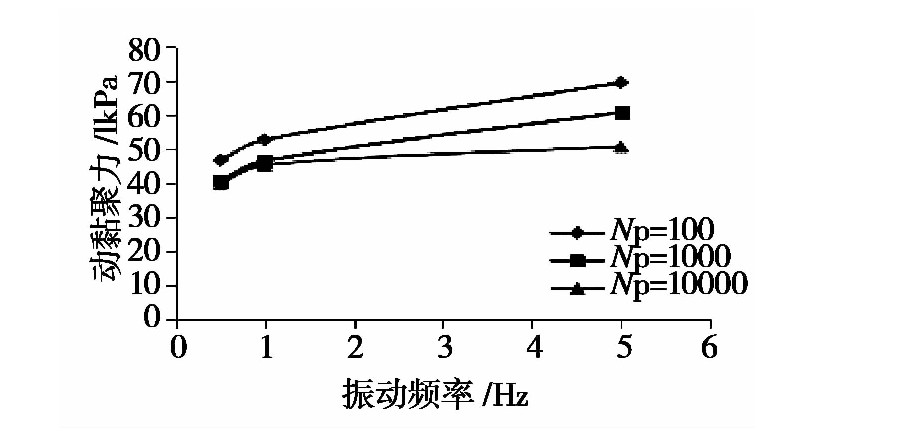
圖6 不同振動頻率下動黏（nián）聚力值

隨著振動（dòng）頻率的（de）增（zēng）加，試件的動內摩擦角值與動黏（nián）聚力值均呈現上升的趨勢，但隨（suí）著振動頻率的逐漸增加，變（biàn）化趨勢逐漸放緩。當處於同一振動頻率時，隨著破壞振（zhèn）動次數的增加，動摩擦（cā）角的規律性較差，而動（dòng）黏（nián）聚力則是（shì）隨破壞振次的提高而降低。

4.2 最大動彈（dàn）性模量

將動力加載第10次（cì）的循環時（shí）的動應力—應變曲線定為該動應力幅值下的滯回圈，通過橢圓擬合，以橢圓兩頂點的連線（xiàn）斜（xié）率定為該動應力幅值（zhí）下的（de）動彈性模量Ed,而土體在受到循環荷載作用下，其動本構關係符合式(1)所列出的雙曲線關係即：

Ed=σdεd=1a+bεd         (1)Ed=σdεd=1a+bεd         (1)

其中：

σd為動應力幅值（zhí）/kPa;

εd為動（dòng）應變/%;

a、b均為土體（tǐ）參數。

由式(1)又可導出：

1Ed=a+bεd         (2)1Ed=a+bεd         (2)

由於各條（tiáo）件下的動彈（dàn）性模量值可由試驗結果計算得到，因此隻要通過對1Ed1Ed進行不同條件（jiàn）下的線性擬合，就（jiù）能夠確定不同條件下（xià）的土體參數a、b,在式(2),εd恒小於1,因此最大動彈（dàn）性模量即為：

Edmax=1a         (3)Edmax=1a         (3)

各條件下最大動彈性模量曲線分別如（rú）見圖7至圖（tú）9所示。

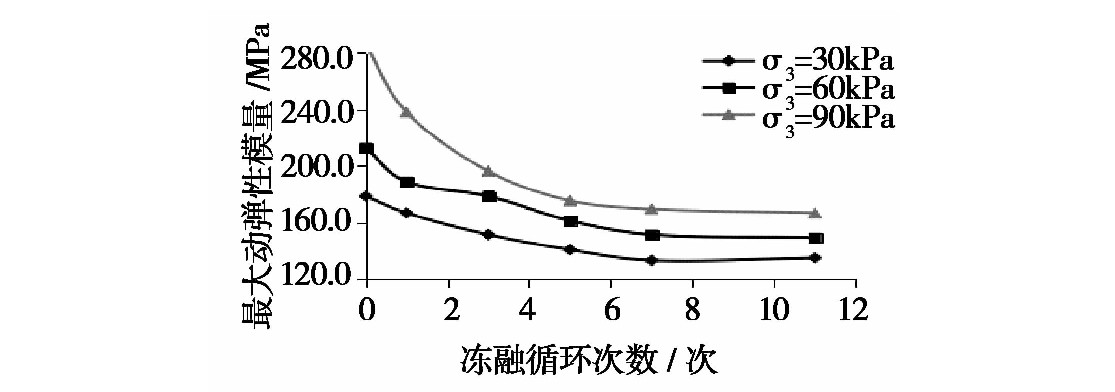
圖7 不同（tóng）凍融循環次數下最大動彈性模量（liàng）曲線

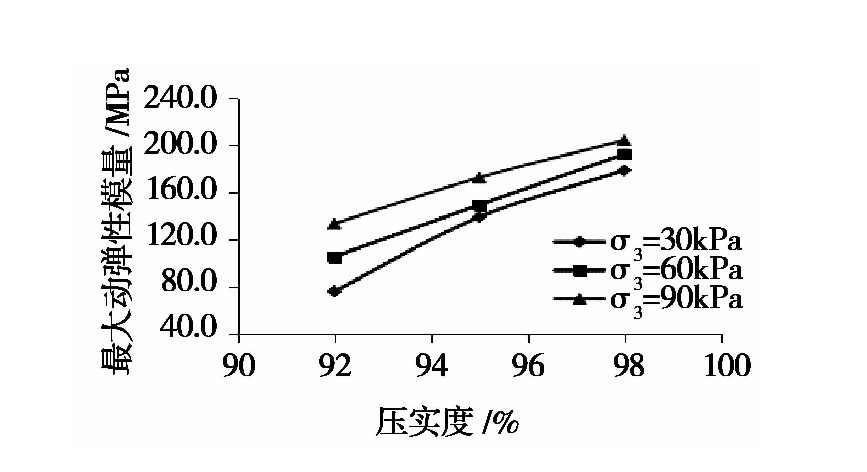
圖8 不同壓實（shí）度下最大動彈性模量曲線

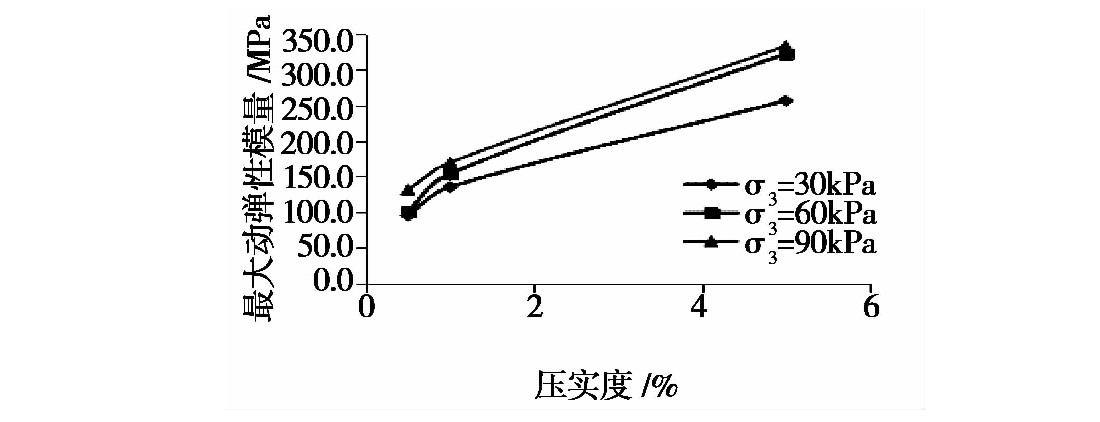
圖9 不（bú）同振動（dòng）頻率下最大動彈性模量曲線

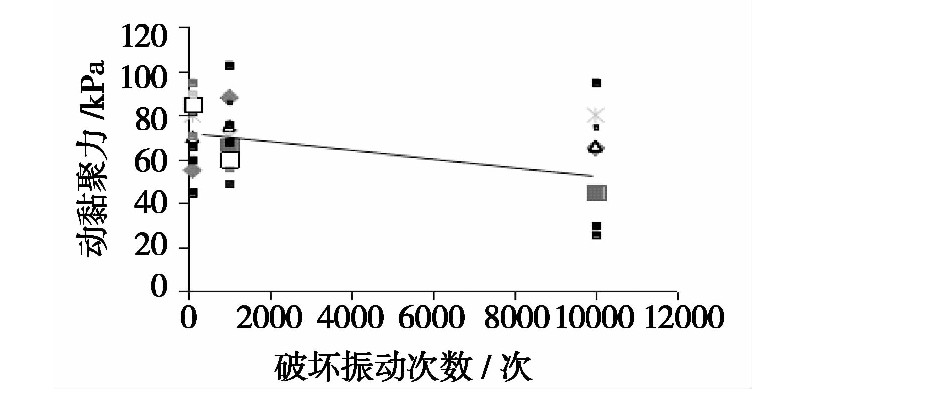
圖10 單一考（kǎo）慮破壞振（zhèn）次（cì）下的動黏聚力標準（zhǔn）值曲線

隨著圍壓水平的（de）增加，試件經受（shòu）不同凍融循環作（zuò）用次數下的最（zuì）大動彈性模量均隨之提高；當圍壓水（shuǐ）平一定時，試件的最大（dà）動彈性（xìng）模量隨凍融循環（huán）作用（yòng）次數的增加而降低，且當凍融循環作用（yòng）次數（shù）為3次時，衰（shuāi）減速（sù）率達到最大，當凍（dòng）融循環作用次數大於5次後，試件的最大動（dòng）彈（dàn）性模量逐漸趨（qū）於平穩；隨著壓實度的提高，試件最大動彈性模量顯著增強；而在不同圍壓水平下，壓實度的提（tí）高對試件最大動（dòng）彈性模量的變化影響有一定的變化，隨著圍壓水平的（de）提高，壓實的提高對試件最大動彈性模量的提升作用減弱；隨著振動頻率的提高，試件的最大動彈性模量增大。

5 動力學參數變化規律的擬合

5.1 動黏聚力(圖10)

以單一受破壞振動（dòng）次數影響（xiǎng）下的動黏聚力擬合值作為標準（zhǔn）值，將其他（tā）各因素的試驗值（zhí）與標準值之比作為個參數下的代表值，采用比值（zhí）法進行驗證。

擬合曲線：

cd0=p1Np+q1 (4)

其（qí）中：

cd0為動黏聚力標準（zhǔn）值；

Np為破壞振動次數/次；

p1、q1為擬合參數(分別為：p1=0.0013,q1=67.772)

凍融循（xún）環次數影響下的動黏聚力代表值擬合曲線(圖11):

cN=cdcd0=p2+q2e−m2Np         (5)cΝ=cdcd0=p2+q2e-m2Νp         (5)

其中：

cN為凍融（róng）循環次數影響下動黏聚（jù）力代表值；

p2、q2、m2為擬合參數(分別為：p2=0.813,q2=0.447,m2=0.362)

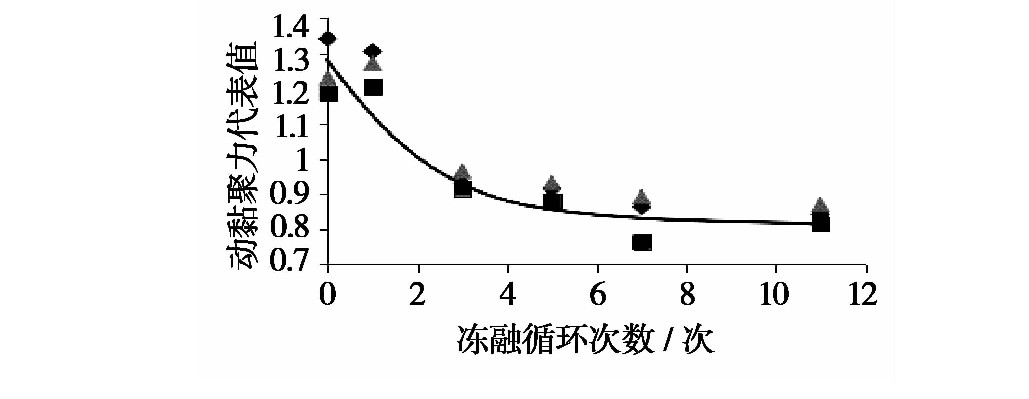
圖11 凍融循環次數影響（xiǎng）下動（dòng）黏聚力代表值擬合

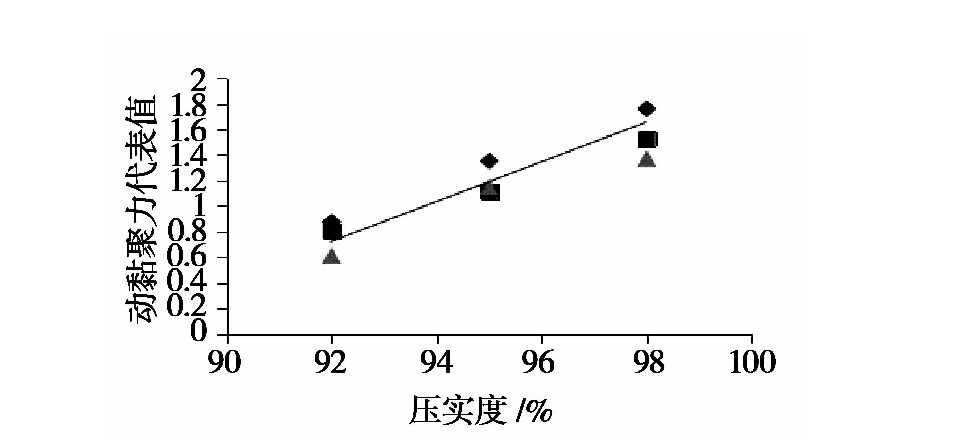
圖12 壓實（shí）度影（yǐng）響下動黏聚力代表值擬（nǐ）合

壓實度（dù）影響下擬合曲線(圖12):

cK=cdcd0=p3ln(K)+q3         (6)cΚ=cdcd0=p3ln(Κ)+q3         (6)

其（qí）中：

cK為壓實度影響下動黏聚力代表值；

p3、q3為擬合參數(分別為：p3=12.015,q3=55.218)。

振動頻率影響下擬合曲線(圖13):

cf=cdcd0=p4f2+q4f+m4         (7)cf=cdcd0=p4f2+q4f+m4         (7)

其中：

cf為考（kǎo）慮振動頻率下的動黏聚力代表值；

p4、q4、m4為擬合參數(分別（bié）為：p4=-0.215,q4=0.113,m4=0.676)。

考慮多重影響（xiǎng）因素下的動黏聚力擬（nǐ）合（hé）公式可采（cǎi）用多元非線（xiàn）性回歸的線性化分析方法進行計算：

cn=pcNcd0+qckcd0+mcfcd0+n (8)

其中：

cn為考慮各項因素後（hòu）的動黏聚力擬合值；

p、q、m、n為調整係數(分（fèn）別為：p=0.731,q=0.699,m=0.105,n=54.118)。

動黏聚力的擬合值分布情（qíng）況如圖14所示。

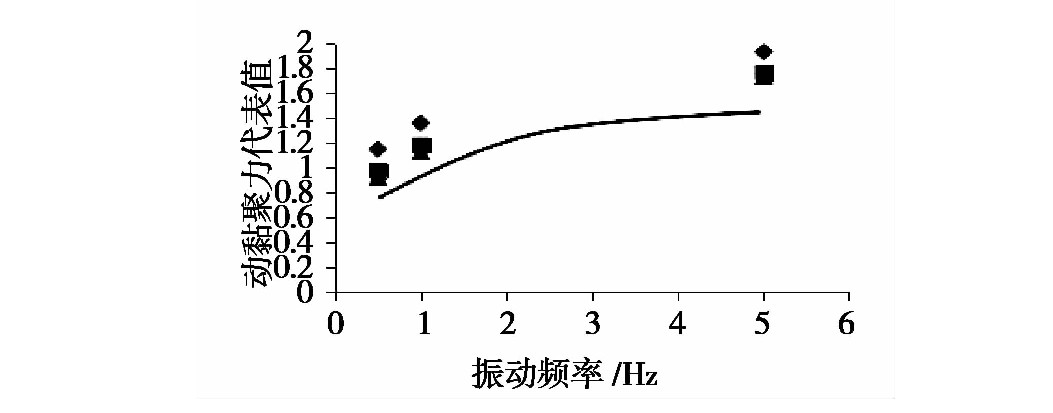
圖（tú）13 振動頻率影響下動黏聚力代表值擬（nǐ）合

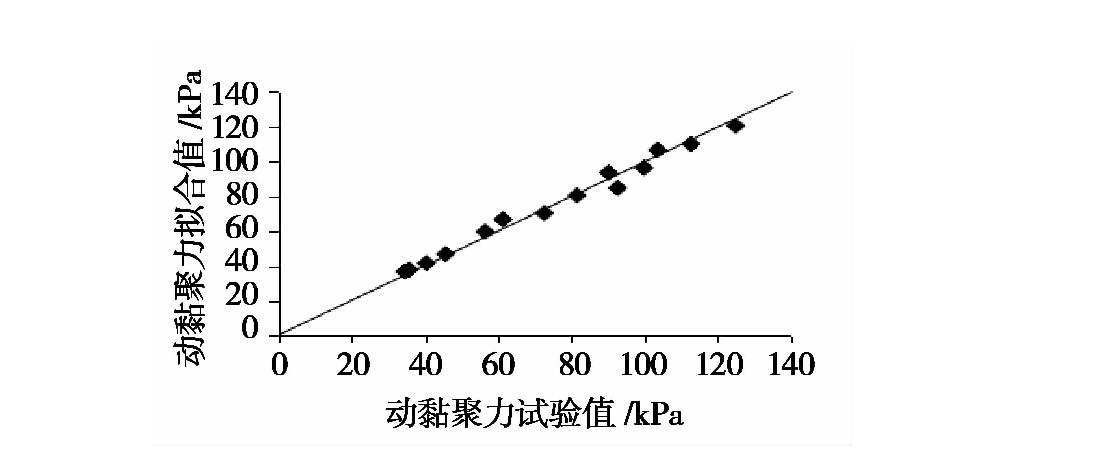
圖（tú）14 動黏聚力的擬合對照驗證

可以看出，擬合（hé）後的動黏（nián）聚力值分布在等值線（xiàn）附近，說明擬合效果良（liáng）好（hǎo）。

5.2 最（zuì）大動（dòng）彈性模量

單（dān）一考慮圍壓條（tiáo）件影響下的最大動彈（dàn）性模量擬合值作為（wéi）標準值，將不同條件影響因（yīn）素下的試驗結果與該值之（zhī）比（bǐ）作為該種影響因素下的最大動彈（dàn）性模量代表值，並對代表值進行非線性擬合。

Ed0=l1σ32+j1σ3+i1 (9)

其中：

Ed0為單一考慮圍壓作用（yòng）下的最大動彈性模量標準值/kPa;

l1、j1、i1為擬合參數(分別為：l1=0.0031,j1=0.460,i1=133.571)

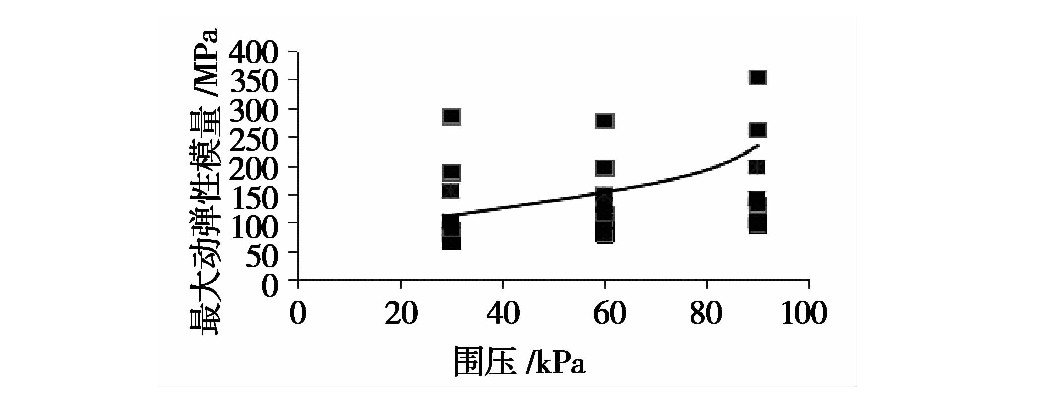
圖15 單一考慮圍壓作（zuò）用下擬合曲線

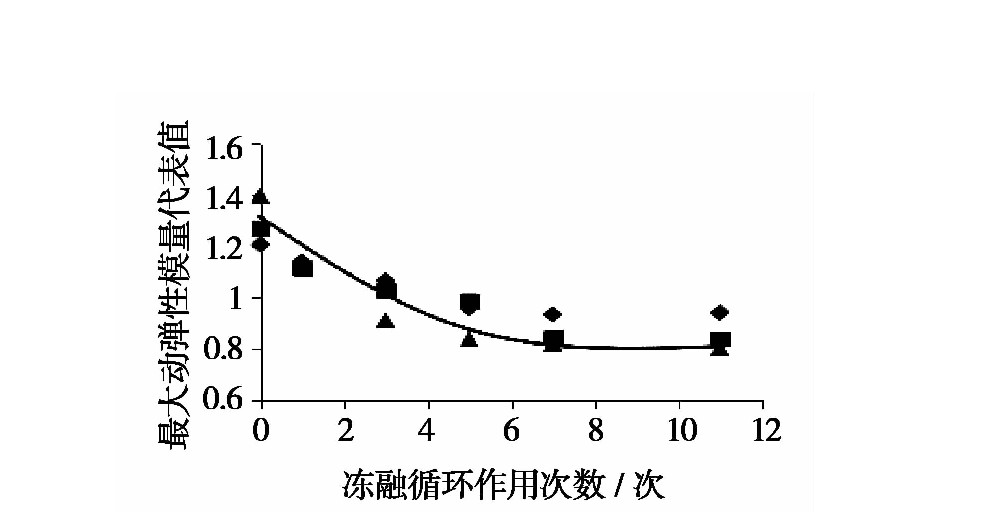
圖（tú）16 凍融循環作用次數影響下（xià）最大動彈性模量代表值擬合曲線

凍（dòng）融循環次數影響下的最大動彈性模量代（dài）表值擬合曲線：

EdN=EdmaxEd0=l2+j2e−i2Nft         (10)EdΝ=EdmaxEd0=l2+j2e-i2Νft         (10)

其中：

EdN為考慮凍融循（xún）環作用次數下的最大（dà）動彈性模量代表（biǎo）值；

l2、j2、i2為擬合參數(分別為：l2=0.850,j2=0.416,i2=0.392)。

壓實度影響下最大動彈性模量代表（biǎo）值擬合曲線：

EdK=EdmaxEdo=l3ln(K)+j3  (11)EdΚ=EdmaxEdo=l3ln(Κ)+j3  (11)

其中：

EdK為（wéi）考慮（lǜ）壓實度影響下的最大動彈性模量代表值；

l3、j3為擬合參數(分別為：l3=12.561,j3=57.330)。

圖（tú）17 壓實度影響下最大動彈性模量代表（biǎo）值擬合曲線

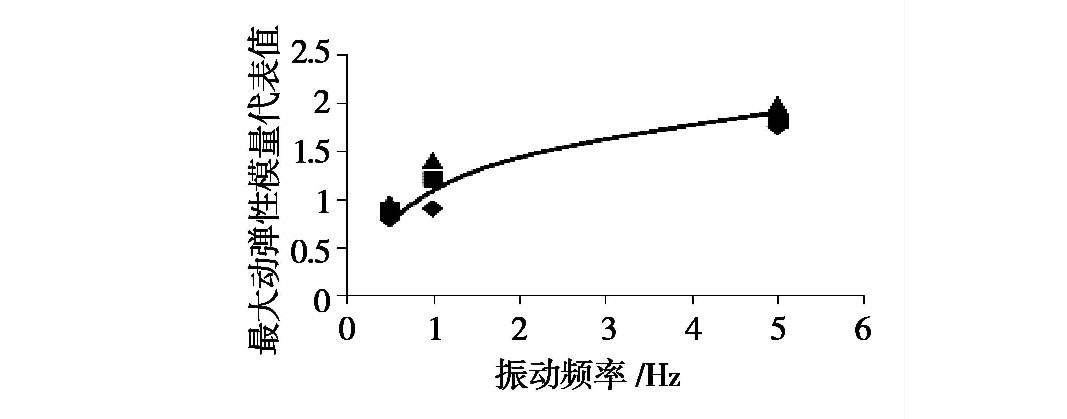
圖18 振動頻（pín）率影響下最大動彈性模量代（dài）表值擬合曲線（xiàn）

曲線用下式（shì）進（jìn）行擬合：

Edf=EdmaxEd0=l4f2+j4f+m4         (12)Edf=EdmaxEd0=l4f2+j4f+m4         (12)

其中：

Edf為考慮振動頻率影響下的最大動彈性模量代表值；

l4、j4、m4為擬合參數(分別為：l4=-0.262,j4=0.815,m4=0.368)。

考慮多重影響因素下（xià）的（de）最大動（dòng）彈（dàn）性模量擬合公式可（kě）采用多元（yuán）非線性回歸的線（xiàn）性化分（fèn）析方法進行計算，采用下式進行擬合：

Edn=l'EdNEd0+j'EdKEd0+p'EdfEd0+q' (13)

其中：

Edn為考慮各因素下的最大動彈性模量擬合值；

l'、j'、p'、q'為調整係數(分別為：l'=0.751,j'=0.363,p'=0.142,q'=-76.381)。

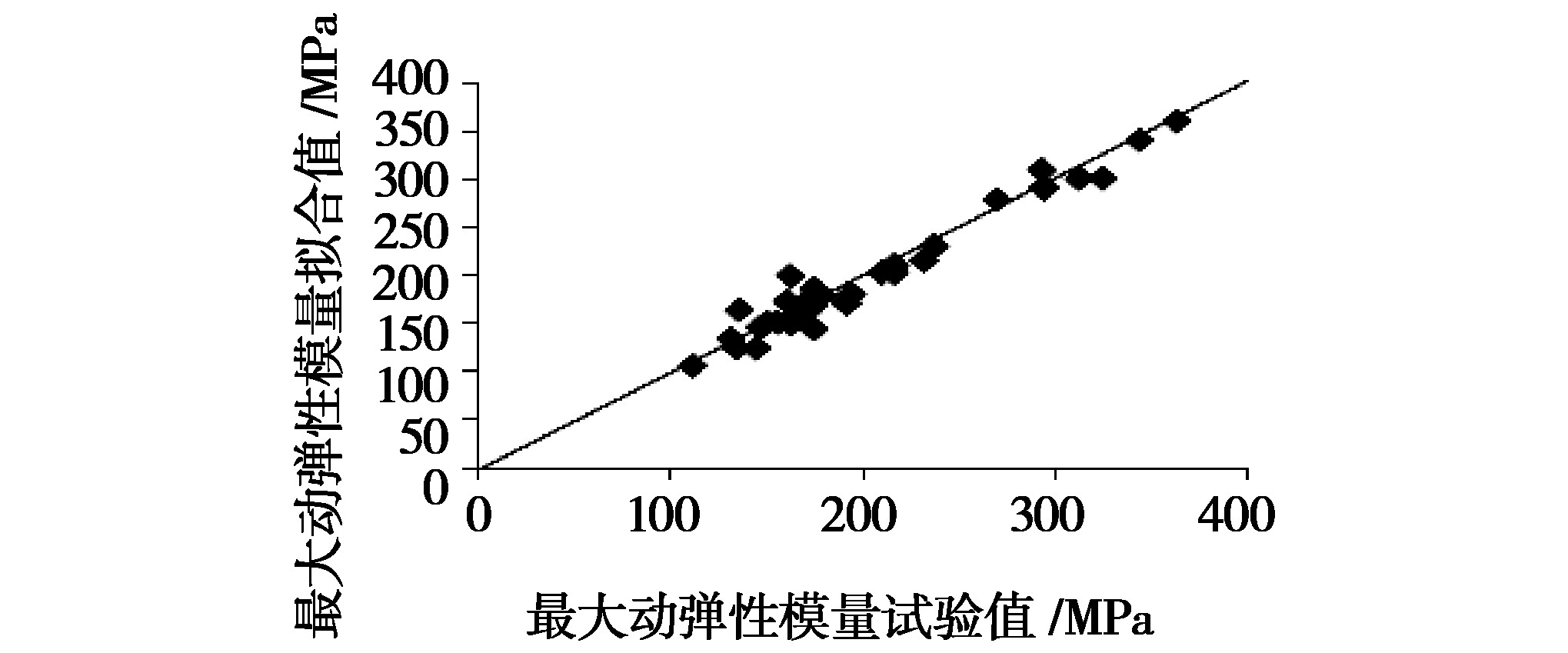
圖19 最大動（dòng）彈性模量的試驗值與擬（nǐ）合值對照（zhào）驗證

最大動彈性模量經式(13)擬合後的取值與（yǔ）試驗（yàn）值對照大多均勻分布在等值線兩側，說明本次針對最大動彈性模量的擬合結果良好。

6 結（jié）論

研究了不同凍融循環作（zuò）用次數、不同壓實度以及不同（tóng）加載振動頻率下試件的各項動力學參數的變化規（guī）律，並（bìng）對不同影響因素下的動力學參數（shù）包括動黏聚力（lì）和最大動（dòng）彈性模量進（jìn）行多元非線（xiàn）性回歸的線性化分析，提出了動（dòng）黏聚力（lì）和（hé）最大動彈性模量的經驗公式，直觀地展現（xiàn）出（chū）不同影響因素下張承高（gāo）速（sù）所在區域即河北省北部、北京西北部地區季凍區路基填（tián）土受凍融循環作用下的（de）變形特性和強度變化規律，了解各個影響因素作用的強弱（ruò），推測各個力學參數在實際變化中（zhōng）的規律和趨勢，為張承高速（sù）及國內類（lèi）似季凍區域（yù）高（gāo）等級公路的建設和運營和維護工作（zuò）提供參考。

參考文獻

[1] 宋金華，李博楠，王亮（liàng），等.凍（dòng）融循環作用下石灰（huī）改良土路（lù）基填料的（de）動力特性研究[J].重慶（qìng）交通大學學（xué）報(自（zì）然科學版),2018,37(2):47-54.

[2] 魏盛昊.凍融作用下路基填土力學特性及變（biàn）形預測研究[D].西安（ān）：西安科技（jì）大學，2020.

[3] 夏夢露.凍融循環作用下路基土變形特性及數值計算分析[D].長春：吉林大學，2020.

[4] 陳洪興，陳景龍.季（jì）凍區路基土抗（kàng）剪強度指標變化規律研（yán）究[J].公路交通技術，2016,32(1):1-5.

[5] 王靜，劉寒冰（bīng），吳春利，等.凍融循環對不同塑性（xìng）指數路基土動力特性影響（xiǎng）[J].岩土工程學報，2014,36(4):633-639.

[6] Yarbasi N,Kalkan E,Akbulut S.Modification of the geotechnical properties,as influenced by freeze-thaw,of granular soils with waste additives[J].Cold Regions Science and Technology,2015,48(1):44-54.

[7] 王威娜，支喜蘭，毛雪鬆（sōng），等.凍融循環作用下路基土回（huí）彈模量試驗研究[J].冰（bīng）川凍（dòng）土，2010,32(5):954-959.

[8] 陳文.季節性冰凍區公路路基濕度與（yǔ）模量（liàng）研究[D].武漢：武漢工業學院，2012.

[9] 侯恩創.凍融循環對路基土物理（lǐ）力學性（xìng）質影響的研究[D].哈爾濱：東北林業大學，2009.

[10] 李晶.對季凍區路基強度及穩定性的試驗研究[J].黑龍江交通科技（jì），2010,33(3):54-55.